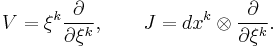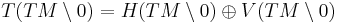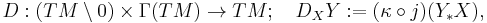Double tangent bundle
In mathematics, particularly differential topology, the double tangent bundle or the second tangent bundle refers to the tangent bundle (TTM,πTTM,TM) of the total space TM of the tangent bundle (TM,πTM,M) of a smooth manifold M [1]. The second tangent bundle arises in the study of connections and second order ordinary differential equations, i.e., (semi)spray structures on smooth manifolds, and it is not to be confused with the second order jet bundle.
Contents |
Secondary vector bundle structure and canonical flip
Since (TM,πTM,M) is a vector bundle on its own right, its tangent bundle has the secondary vector bundle structure (TTM,(πTM)*,TM), where (πTM)*:TTM→TM is the push-forward of the canonical projection πTM:TM→M. In the following we denote
and apply the associated coordinate system
on TM. Then the fibre of the secondary vector bundle structure at X∈TxM takes the form
The canonical flip[2] is a smooth involution j:TTM→TTM that exchanges these vector space structures in the sense that it is a vector bundle isomorphism between (TTM,πTTM,TM) and (TTM,(πTM)*,TM). In the associated coordinates on TM it reads as
Canonical tensor fields on the tangent bundle
As for any vector bundle, the tangent spaces Tξ(TxM) of the fibres TxM of the tangent bundle (TM,πTM,M) can be identified with the fibres TxM themselves. Formally this is achieved though the vertical lift, which is a natural vector space isomorphism vlξ:TxM→Tξ(TxM) defined as
The vertical lift can also be seen as a natural vector bundle isomorphism vl:(πTM)*TM→VTM from the pullback bundle of (TM,πTM,M) over πTM:TM→M onto the vertical tangent bundle
The vertical lift lets us define the canonical vector field
which is smooth in the slit tangent bundle TM\0. The canonical vector field can be also defined as the infinitesimal generator of the Lie-group action
Unlike the canonical vector field, which can be defined for any vector bundle, the canonical endomorphism
is special to the tangent bundle. The canonical endomorphism J satisfies
and it is also known as the tangent structure for the following reason. If (E,p,M) is any vector bundle with the canonical vector field V and a (1,1)-tensor field J that satifies the properties listed above, with VE in place of VTM, then the vector bundle (E,p,M) is isomorphic to the tangent bundle (TM,πTM,M) of the base manifold, and J corresponds to the tangent structure of TM in this isomorphism.
There is also a stronger result of this kind [3] which states that if N is a 2n-dimensional manifold and if there exists a (1,1)-tensor field J on N that satisfies
then N is diffeomorphic to an open set of the total space of a tangent bundle of some n-dimensional manifold M, and J corresponds to the tangent structure of TM in this diffeomorphism.
In any associated coordinate system on TM the canonical vector field and the canonical endomorphism have the coordinate representations
(Semi)spray structures
A Semispray structure on a smooth manifold M is by definition a smooth vector field H on TM \0 such that JH=V. An equivalent definition is that j(H)=H, where j:TTM→TTM is the canonical flip. A semispray H is a spray, if in addition, [V,H]=H.
Spray and semispray structures are invariant versions of second order ordinary differential equations on M. The difference between spray and semispray structures is that the solution curves of sprays are invariant in positive reparametrizations as point sets on M, whereas solution curves of semisprays typically are not.
Nonlinear covariant derivatives on smooth manifolds
The canonical flip makes it possible to define nonlinear covariant derivatives on smooth manifolds as follows. Let
be an Ehresmann connection on the slit tangent bundle TM/0 and consider the mapping
where Y*:TM→TTM is the push-forward, j:TTM→TTM is the canonical flip and κ:T(TM/0)→TM/0 is the connector map. The mapping DX is a derivation in the module Γ (TM) of smooth vector fields on M in the sense that
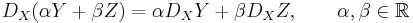 .
.![D_X(fY) = X[f]Y %2B f D_XY, \qquad \qquad \qquad f\in C^\infty(M)](/2012-wikipedia_en_all_nopic_01_2012/I/972cc8a910302750b071394963177830.png) .
.
Any mapping DX with these properties is called a (nonlinear) covariant derivative [4] on M. The term nonlinear refers to the fact that this kind of covariant derivative DX on is not necessarily linear with respect to the direction X∈TM/0 of the differentiation.
Looking at the local representations one can confirm that the Ehresmann connections on (TM/0,πTM/0,M) and nonlinear covariant derivatives on M are in one-to-one correspondence. Furthermore, if DX is linear in X, then the Ehresmann connection is linear in the secondary vector bundle structure, and DX coincides with its linear covariant derivative if and only if the torsion of the connection vanishes.
See also
References
- ^ J.M.Lee, Introduction to Smooth Manifolds, Springer-Verlag, 2003.
- ^ P.Michor. Topics in Differential Geometry, American Mathematical Society, 2008.
- ^ D.S.Goel, Almost Tangent Structures, Kodai Math.Sem.Rep. 26 (1975), 187-193.
- ^ I.Bucataru, R.Miron, Finsler-Lagrange Geometry, Editura Academiei Române, 2007.
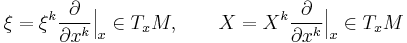
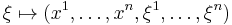
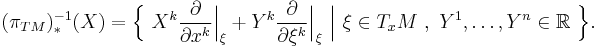
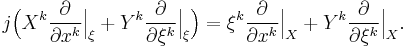
![(\operatorname{vl}_\xi X)[f]:=\frac{d}{dt}\Big|_{t=0}f(x,\xi%2BtX), \qquad f\in C^\infty(TM).](/2012-wikipedia_en_all_nopic_01_2012/I/740d65dd948b614318435d33e58d95fe.png)
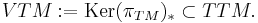
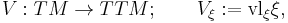
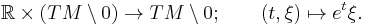
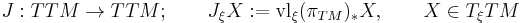
![\operatorname{Ran}(J)=\operatorname{Ker}(J)=VTM, \qquad \mathcal L_VJ= -J, \qquad J[X,Y]=J[JX,Y]%2BJ[X,JY],](/2012-wikipedia_en_all_nopic_01_2012/I/8950de0d42e957e96c1dacbf93fe9412.png)
![\operatorname{Ran}(J)=\operatorname{Ker}(J), \qquad J[X,Y]=J[JX,Y]%2BJ[X,JY],](/2012-wikipedia_en_all_nopic_01_2012/I/6ac831537d02e2c586777f43a0d4574f.png)